Fitts's law

Fitts’ Law can be described as “The time required to move to a target is a function of the target size and distance to the target.” We can apply this to web design by looking at the hit area of our objects. Meaning the larger we can make the clickable area of key links and navigational elements the easier they will be to click on. Remember that while as web designers we may be extremely proficient at using the mouse and the web, there are a lot of users who still have trouble with these basic functions.

Fitts’ law is a model of human movement which predicts the time required to rapidly move to a target area, as a function of the distance to the target and the size of the target. The law is usually applied to the movement of the mouse visitors have to perform to get from point A to point B. For instance, the rule can be important to place the content areas in a more usable way to maximize their accessibility and improve click rates.

A common misuse of Fitts’ law is when a design is coded so that the text of a menu bar is clickable but the tabs themselves are not. Rather than just making the text clickable it would be a great idea to add padding to that link element to increase the clickable area. Sometimes this means turning the anchor into a block level element and wrapping details inside.

This can work in the opposite way as well, meaning items we want to be difficult to be clicked on (such as cancel buttons / links) should have a smaller clickable area. This is why you often see forms or actions that have large “save” buttons but text based “delete” or “cancel” links.

Fitts' law is a model of human movement primarily used in human–computer interaction and ergonomics that predicts that the time required to rapidly move to a target area is a function of the distance to the target and the size of the target.

T = a + b log2(1 + D/W)

where:

• T is the average time taken to complete the movement. (Traditionally, researchers have used the symbol MT for this, to mean movement time.)
• a represents the start/stop time of the device (intercept) and
• b stands for the inherent speed of the device (slope). These constants can be determined experimentally by fitting a straight line to measured data.
• D is the distance from the starting point to the center of the target. (Traditionally, researchers have used the symbol A for this, to mean the amplitude of the movement.)
• W is the width of the target measured along the axis of motion. W can also be thought of as the allowed error tolerance in the final position, since the final point of the motion must fall within ±^W⁄₂ of the target's center.

From the equation, we see a speed–accuracy trade off associated with pointing, whereby targets that are smaller and/or further away require more time to acquire.

Visualizing Fitts’s Law by Kevin Hale

Introduction

In preparation for the redesigns and overhauls we implemented in Wufoo, I took some time to revisit a few HCI (Human-Computer Interaction) fundamentals with the hopes of gleaning something new out of the decades of research dedicated to making interfaces easier to use. One thing that surprised me was how most of the material was pretty dense, heavily geared towards mathematicians it seemed and written in the impenetrable language of the academic elite. You’d think that if they’d really wanted to make an impact (especially on designers), they’d create documents that were a bit easier to digest.

Back in school, I remember that it wasn’t until I started taking classes in physics that calculus made any kind of real sense to me. I just need diagrams to function. In that spirit, I thought it would be nice to go over Fitts’s Law, a staple in the HCI diet, with a few visuals to explain both the concept and why it’s ideas are a bit more complicated than most would have you believe.

Math of the Obvious

Published in 1954, Fitts’s Law is an effective method of modeling the relationship of a very specific, yet common situation in interface design. That situation involves a human-powered appendage at rest (whether it’s physical like your finger or virtual like a mouse cursor) and a target area that’s located somewhere else. Here’s diagram the first:

Mathematically, Fitts’s law is stated as follows:

MT = a + b log2(2A/W)

Basically, that means that the time to acquire a target is a function of the distance to and size of the target. It seems like a no brainer. The farther you are and the smaller the target, the longer it takes to move the cursor and point at said target. However, Tom Stafford said it best:

“Although the basic message is obvious (big things are easier to select) it is the precise mathematical characterization that is exciting, and that this characterization includes a logarithmic function - which means that the shape of the relationship between size and reaction time is curved so that small increases in size for small objects make it much easier to select them (whereas small increases in size for big objects don’t make that much difference). And the same applies for changes in target distance.”

Size and selection times: Fitts’s Law

Just to bring it into the real world, this makes sense since a penny is a lot easier to point at than a freckle and a house is just as easy to point at as an apartment complex. So the next time you optimize your web site based on Fitts’s Law, remember that if your link is already huge, making it “huger” will not significantly increase the speed at which one can access it. However, making tiny links a little bigger does make a difference.

Fitts’s Law is Made of Lines!

Wanting to find practical lessons from Fitts’s equation, interface designers have derived a few rules of best practice to take advantage of one of the very few laws of human interaction. One rule, The Rule of Target Size, combines ideas behind Fitts’s Law and Hick’s Law (a law I’ll talk about on a later date) to state that the size of a button should be proportional to its expected frequency of use. Bruce “Tog” Tognazzini of Apple interface fame even developed an excellent quiz to explain how Fitts’s Law can be used to develop rules to drastically improve operating system interfaces.

Before you go and follow these rules blindly in your applications, I want to remind you that Fitts’s Law describes a very specific situation. There is an assumption that the movement from the starting position is rapid and aimed, which means it’s always in a straight line and confident (starts with high initial velocity as if there were no other targets and you knew exactly where you needed to go). Also, I’ve seen a lot of people think Fitts’s Law describes the following situation:

However, in the equation shown above, there’s no variable for height of the target area, only width. And so one of the most talked about limitations of Fitts’s law in HCI circles is that it predicts movement in only one dimension. In Fitts’s original experiments, he actually only tested human performance in making horizontal moves toward a target. Both the amplitude of the move and the width of the terminating region were measured along the same axis, which means the model it describe looks more like this:

Now, if we were to base link size optimizations solely on Fitts’s Law and we assume that vertical and diagonal movements can be described using the same equation, then the ease at which you can point to a specific target actually depends on where your starting position is in relation to your target.

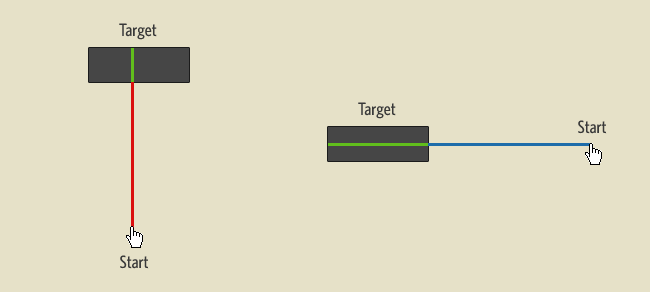
In the example above, the cursor on the right will technically have an easier time selecting the target than the cursor on the left since it will have more “target width” to work with. Notice that Fitt’s Law would work fine for circular targets since the width to the center of the object would be the same from all angles. However, it becomes less accurate for rectangular targets and even more so for irregular objects. In the next example, we’ll look at two attempts to optimize the target area of a link by increasing rectangular dimensions.

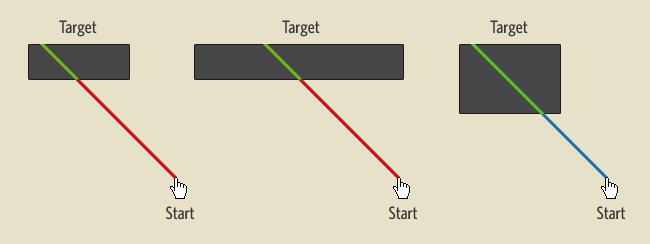
The second figure increases the width of the target box and the third increases the height. As you can see, based on where the mouse cursor starts, not all size increases on a rectangular target result in an easier target acquisition, which could be significant for web designers considering all CSS designs are based on the Box Model.

Physical vs Virtual Pointing

Hundreds of derivative experiments have been performed since the publication of Fitts’s findings. One interesting paper from 1996 by Evan Graham and Christine MacKenzine, analyzed differences between how well we pointed at objects in real space versus objects on the computer screen. They show that the movement from the starting point to the target area could be divided into two parts: the initial high velocity phase and a deceleration phase.

In their study, they discovered that the first phase was only affected by the distance away from the target. The scale of the display nor the size of an object didn’t make you approach it more quickly from the start (bigger links don’t make you more eager). The phase that actually affects the time to select a smaller object at the same distance, is in the deceleration phase. Now, here’s the “interesting” part:

“The difference between the virtual and physical display is apparent only in the second movement phase, where visual control of deceleration to the smaller targets in the virtual task took more time than in the physical task.”

Basically, links and buttons on a screen are harder to point out with your mouse than with your finger. And the problem with mice apparently is not in their ability to get to the target, but in our ability to decelerate accurately with them. Apple, I eagerly wait for the release of some multi-touch monitor goodness.

Rule of the Infinite Edge

It turns out that computer monitors add a very interesting twist to Fitts’s model of target selection, because they have something called “edges.” Jeff Atwood of Coding Horror actually explained this rather excellently last year in an article on Fitts’s Law and Infinite Width. Because a pointing device can only go so far in any direction, targets at the edge of the screen technically have infinite target widths as illustrated below.

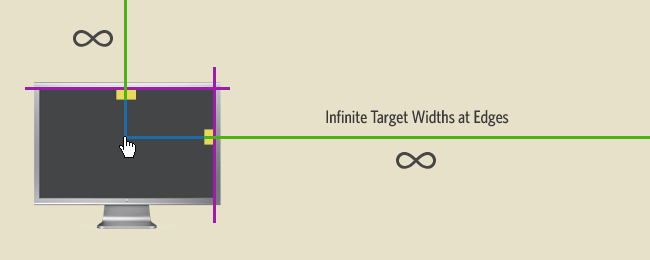
For an operating system and on any full screen application, these edges are usually considered the most valuable real estate since they are technically the most accessible. Not only do they have infinite widths, they also don’t require the user to have a deceleration phase when they approach these targets, since the edge of the screen will just stop them. This is also why it’s incredibly fast and intuitive to assign actions like Expose and Dashboard to the corners of a screen.

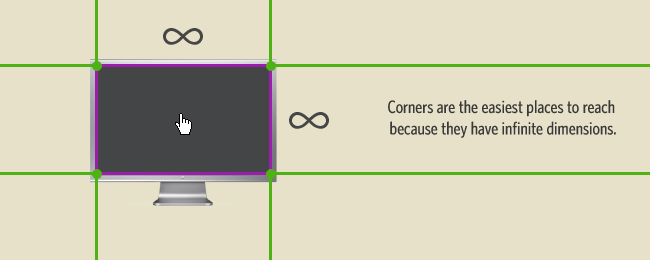
Unfortunately, web applications do not get to benefit from the Rule of Infinite Edges. Having the limitation of needing to run in a browser window with borders, it’s of little value according to Fitts’s Law for web designers to place buttons and links at the edges and corners unless the browser is running at full screen, which seems to only happen for kiosk applications.

This also might explain why the interfaces of Web Operating Systems will never be as good as those that can take advantage of the entire real estate of your monitor.

Fitts Still Rules!

The few limitations of Fitts’s Law that I’ve presented here are not an attempt to have you throw its lessons out the window. My hope is that by illustrating some of the debates, it’ll show you how something as simple as pointing at something is just as relevant and debatable now as it was over 50 years ago. And while it’s technically not an accurate description of most interface situations—humans don’t always move confidently to a target, we don’t move in only straight lines, there are usually several targets that can confuse us and target areas are almost always two dimensional—research that has created a more accurate mathematical model that compensates for 2 and even 3 dimensions, hardware noise, human error and a host of other factors doesn’t seem to change the fundamental truths behind Fitts’s rather versatile equation:

“Fitts’s law has been shown to apply under a variety of conditions, with many different limbs (hands, feet, head-mounted sights, eye gaze), manipulanda (input devices), physical environments (including underwater!), and user populations (young, old, mentally retarded, and drugged participants).”

In the end, the big idea I’d like designers to take away from this article is that the challenge of software application design is so complex and filled with so many variables, that blanket solutions derived from Fitts’s Law should be used cautiously. With the increasing size of monitors, the rising popularity of variables that increase mouse acceleration and technologies that alter how we scroll through large screens, it’ll be interesting see how software designers will take advantage of tools that let us augment our ability to close large distances quickly.

A Quiz Designed to Give You Fitts

So you think you are an interaction designer? Not if you cannot answer all the following questions quickly and with authority.

If you're not an interaction designer, but you know one—or you are thinking of hiring one—slip them just the questions, and see how well they do. I've used variations of this quiz for years during the interview process to good effect.

These questions and answers assume that you have total control over all screen real estate, the OS, etc. Just pretend you are chief designer for Microsoft or Apple.

If you are new to matters Fitts, take the quiz before looking at the text the follows anyway. The answers are going to thoroughly teach the principles involved, but taking your best shot at the quiz first will make clear to you what assumptions you have been using in the past. You can then measure those assumptions against the answers that follow. And don't feel bad with your initial results: The overwhelming majority of people, even those that have been involved with computers for years, do poorly on their first time around. The good news is that they do great on the retake, and many have found this the most valuable single article on this website, immediately and permanently applicable to their future design work.

The Quiz

You may want to read through all the questions (but not the answers!) once just to get the "lay of the land." Then, go back and answer them. And you really do have to answer them. This is not a quiz that lends itself to looking at a question and saying, “Oh, yeah, sure. I know that one,” and scanning on down. You have to actually articulate the answer. (Otherwise, you are considered to have gotten it wrong.)

No tricks are hiding within. This is all straight business. However, the answers may seem counter-intuitive or counter-experiential, so apparent "obviousness" might not suffice.

1. Microsoft Toolbars offer the user the option of displaying a label below each tool. Name at least one reason why labeled tools can be accessed faster. (Assume, for this, that the user knows the tool and does not need the label just simply to identify the tool.)
2. You have a palette of tools in a graphics application that consists of a matrix of 16x16-pixel icons laid out as a 2x8 array that lies along the left-hand edge of the screen. Without moving the array from the left-hand side of the screen or changing the size of the icons, what steps can you take to decrease the time necessary to access the average tool?
3. A right-handed user is known to be within 10 pixels of the exact center of a large, 1600 X 1200 screen. You will place a single-pixel target on the screen that the user must point to exactly. List the five pixel locations on the screen that the user can access fastest. For extra credit, list them in order from fastest to slowest access.
4. Microsoft offers a Taskbar which can be oriented along the top, side or bottom of the screen, enabling users to get to hidden windows and applications. This Taskbar may either be hidden or constantly displayed. Describe at least two reasons why the method of triggering an auto-hidden Microsoft Taskbar is grossly inefficient.
5. Explain why a Macintosh pull-down menu can be accessed at least five times faster than a typical Windows pull-down menu. For extra credit, suggest at least two reasons why Microsoft made such an apparently stupid decision.
6. What is the bottleneck in hierarchical menus and what techniques could make that bottleneck less of a problem?
7. Name at least one advantage circular popup menus have over standard, linear popup menus.
8. What can you do to linear popup menus to better balance access time for all items?
9. The industrial designers let loose on the Mac have screwed up most of the keyboards by cutting their function keys in half so the total depth of the keyboard was reduced by half a key. Why was this incredibly stupid?
10. What do the primary solutions to all these questions have in common?

If you can’t answer the last question, you are going to have all kinds of trouble with the rest. You aren’t alone, of course, as evidence abounds that no one at Microsoft and fewer and fewer people at Apple could answer these questions.

Microsoft sort of has an excuse. They claimed from the beginning that a visual interface with the mouse and all that junk is inferior to a keyboard interface. They might have looked foolish if they had ever really tried to build a real GUI. By consistently sabotaging the visual interface, they have avoided such embarrassment.

What has happened at Apple is a little more mysterious. The industrial-design blunders are expected. Apple’s outside industrial designers have always hovered between cluelessness and hostility when it came to human factors. However, lately, Apple has been doing some pretty stupid stuff in-house, too. Like turning the rapid-access Labels menu into a hierarchical, slowing it down by five or ten times.

The Answers

Let's start out with a preview of the answer to question 10, Fitts' law, since all the others revolve around it. From First Principles of Design:

• Fitts' Law: The time to acquire a target is a function of the distance to and size of the target.

This little bit of obviousness is so often ignored, I sometimes wonder if it is on purpose. Usually, though, it is merely a leading indicator of overall ignorance, amplified by superstition and unsullied by facts or study.

Fortunately, readers of AskTog, being as tenacious as they are perspicacious, either know exactly what Fitts' Law is or will before they go to bed tonight.

Fitts' Law (properly spelled "Fitts's," per the rules of American English, though rarely done so) is simple, absolute, and immutable. Let's see how it pertains to the questions:

Question 1

Here are two answers. You may have more.

1. The label becomes part of the target. The target is therefore bigger. Bigger targets, all else being equal, can always be acccessed faster. Fitts' Law.
2. When labels are not used, the tool icons crowd together.

At first glance, it might appear advantageous to crowd the icons together, since it results in less distance among targets. However, the task here is not to hop from target to target. Instead, the point of origin when a user decides to access the toolbar will usually be somewhere in the content region, away from all the targets.

When the icons are spread apart, users have a "buffer zone" between icons, where an incorrect acquisition will result in no action. When the targets are crowded together, however, the user has more chance to initiate an unwanted action. To avoid this possibility, non-label users learn to slow way down. (Don't bother to ask them whether they've slowed down. They'll tell you it sped them up. Only the stopwatch knows for sure.)

Another way to make the targets bigger, of course, is to always choose large icons, rather than small. Pity the "power-user" with the 4x4-pixel icons who thinks he's going faster.

Question 2

Two separate steps may be necessary to average tool access time. Both are important.

1. Change the array to 1X16, so all the tools lie along the edge of the screen.
2. Ensure that the user can click on the very first row of pixels along the edge of the screen to select a tool. There should be no buffer zone.

This second step is vital, and is so often ignored.

Remember that Fitts' Law states that access time is a function of distance and target size. If the target size is larger, then the time is reduced. It is reduced for a simple reason: the user need not slow down when approaching the target for fear of overshooting.

Now consider the screen edge. How deep is the target? If it were really only the one pixel it appears, it would be very hard to hit. However, the screen edge is, for all practical purposes, infinitely deep. It doesn't matter how fast that mouse is going when it hits the screen edge, that pointer absolutely will not overshoot. Having to hit a pixel two pixels in from the screen edge takes much longer than hitting the edge itself. Use that edge. It is your friend.

Question 3

No, this is not a trick question. And the first part should be immediately answerable by any interaction designer. The extra credit question is not quite as simple. But first, the locations of the five "magic pixels":

The prime pixel is located at the current location of the mouse pointer. Popup menus make use of this pixel, showing up relative to the mouse pointer, no matter where the user may have moved it. This pixel requires zero travel and is, in effect, an infinitely large target—you just can't miss it.

The other four pixels are located, on average, as far away from the mouse pointer as you can get. Their distance, however, is more than made up for by their target size, which is infinite in two dimensions. These magic pixels are the four corners of the screen. Throw the mouse in any direction you desire and the odds are overwhelming that if you threw it with enough velocity, it will end up in one of those four corners. This presupposes a properly designed acceleration function for the mouse.

The key to the extra credit question is in the user's right-handedness. A right-handed user can access, in order of increasing difficulty, and starting with the point already mentioned:

1. The pixel immediately at the current cursor location: Click the mouse and you're done.
2. The bottom-right corner.
3. The top-left corner.
4. The top-right corner.
5. The bottom-left corner.

If you hold the mouse in your right hand and move the mouse, using just your wrist and hand, in the four different directions, you will see how the mechanics of your arm leads to this. The answers for a left handed person are, of course, reversed.

These differences are relatively small compared to the power of the "magic pixels." All four corners should be used and used well.

Question 4

Now these should have started getting easier.

1. Screen edges are prime real estate. You don't waste an entire edge that could be housing a couple of dozen different fast-access icons just for one object, the Taskbar.
2. The auto-hidden Taskbar is entirely too easy to display by accident. Users are constantly triggering it when trying to access something that is close to, but not at, the edge.
3. The Taskbar would not have any of these problems, yet be even quicker to get to if it were located at any one of four corners of the display. Throw the mouse up and to the left, for example, and you'll have a taskbar displayed. Fast access without the false triggering.

Question 5

Microsoft, Sun, and others have made the decision to mount the menu bar on the window, rather than at the top of the display, as Apple did. They made this decision for at least two reasons:

1. Apple claimed copyright and patent rights on the Apple menu bar
2. Everyone else assumed that moving the menu bar closer to the user, by putting it at the top of the window, would speed things up.

Phalanxes of lawyers have discussed point 1. Let's deal with point two. The Apple menu bar is a lot faster than menu bars in windows. Why? Because, since the menu bar lies on a screen edge, it has an infinite height. As a result, Mac users can just throw their mice toward the top of the screen with the assurance that it will never penetrate and disappear.

Unless, of course, I'm testing them at the time. I did a test at Apple where I mounted one monitor on top of another, with the menu bar at the top of the lower display. The only way the user could get to the top monitor was by passing through the menu bar enroute.

I then gave users the task of repeatedly accessing menu bar items. When they first started out, they penetrated into the upper screen by around nine inches on average, just because their mouse velocity was so high. Then they learned they had to slow down and really aim for the menu. By the time they adjusted, their menu-access times became so ponderously slow, they took around the same time as the average Windows user.

The other "advantage" usually ascribed to a menu bar at the top of each window is that users always know where to look for the items pertaining to the task they are carrying out. This is silly. Users may do various tasks within a given window, and the menu items may change. Not only that, but a great many perverse applications exist, particularly in the Sun world, where the menu bar you need to access is not even in the window in which you are working! That is truly bizarre and mind-bending.

Microsoft applications are beginning to offer the possibility, in full-screen mode, of a menu bar at the top of the display. Try this out in Word or Excel. It is much faster. Microsoft's general cluelessness has never been so amply displayed, however, as it is in Microsoft Visual Studio, which has a menu bar at the top of the screen with a one-pixel barrier between the screentop and the menu. Talk about snatching defeat from the jaws of victory.

Question 6

The bottleneck is the passage between the first-level menu and the second-level menu. Users first slide the mouse pointer down to the category menu item. Then, they must carefully slide the mouse directly across (horizontally) in order to move the pointer into the secondary menu.

The engineer who originally designed hierarchicals apparently had his forearm mounted on a track so that he could move it perfectly in a horizontal direction without any vertical component. Most of us, however, have our forarms mounted on a pivot we like to call our elbow. That means that moving our hand describes an arc, rather than a straight line. Demanding that pivoted people move a mouse pointer along in a straight line horizontally is just wrong. We are naturally going to slip downward even as we try to slide sideways. When we are not allowed to slip downward, the menu we're after is going to slam shut just before we get there.

The Windows folks tried to overcome the pivot problem with a hack: If they see the user move down into range of the next item on the primary menu, they don't instantly close the second-level menu. Instead, they leave it open for around a half second, so, if users are really quick, they can be inaccurate but still get into the second-level menu before it slams shut. Unfortunately, people's reactions to heightened chance of error is to slow down, rather than speed up, a well-established phenomenon. Therefore, few users will ever figure out that moving faster could solve their problem. Microsoft's solution is exactly wrong.

When I specified the Mac hierarchical menu algorthm in the mid-'80s, I called for a buffer zone shaped like a <, so that users could make an increasingly-greater error as they neared the hierarchical without fear of jumping to an unwanted menu. As long as the user's pointer was moving a few pixels over for every one down, on average, the menu stayed open, no matter how slow they moved. (Cancelling was still really easy; just deliberately move up or down.) Apple hierarchicals were still less efficient than single level menus, because of the added target, but at least they were less challenging than the average video game.

Sadly, the NeXT folks, when coming to Apple, copied Windows, rather than the Mac, in designing the hierarchical menu interface for OSX. Today's Mac hierarchicals are just as difficult to use as those of Windows.

Fitts' law is not just about target size and distance; it's also about the number of targets. The more targets, all else being equal, the longer the task will take. Hierarchicals automatically add one extra target. Making it difficult to enter a second-level menu adds an additional target, the second-level menu itself.

With my hierarchicals on the pre-OSX Macs, in most cases, the user did not even have to think about targetting the second-level menu. The menu opened, and the user simply aimed for the desired item. The only time the user had to consider the second-level menu separately was when there were so many items in the menu that the one the user was after was way up or way down the list, out of range of the allowable pivot for entry. Even then, users would typically arc along a more radical curve to reach their items in a single motion, rather than breaking things down into the jerky Etch-A-Sketch types of moves users typically make with today's hierarchicals.

When designing a user's required motions, reduce the number of motions needed along with both distance and required precision for each motion, then consider how your proposed scheme maps onto a human's ability to make those motions.

Question 7

With the options displayed around you in a circle, you need only move a pixel or two to enter the "slice of pie" you want. Less travel, good target size. Good design.

They have a second advantage of feeding not only distance, but direction information into your motor memory. As long as the options are few enough, you will soon learn to move your mouse up and to the left to print, down and to the right to fax, etc. In fact, once these simple gestures are learned, you needn't even display the menu anymore, unless the user hesitates long enough to indicate they may be unsure. (This was borne out during the course of the Fabrik project at Apple in the late 1980s.)

Question 8

You can "Fittsize" them by making those items farther away from the mouse pointer larger. They need not literally be larger, since the user is not having any trouble seeing the farther items. Instead, the mapping of mouse-to-screen could be such that, as the user pulls further down the menu, more movement of the mouse is necessary to get a corresponding movement of the pointer. In effect, you are decoupling the behavioral map of the screen from the visual map.

Other decoupling tricks include setting up local gravity, so that once a mouse pointer gets near the target, it is drawn to the target. Barriers can be erected, so that once the mouse enters an object, it is difficult for it to pass through to the other side. This can be frustrating. Having a pressure-sensitive mouse that could "push through" if pushed down upon would enable the user either to be caught by the object or to flee to the territory beyond. Reader Victor Zambrano has suggested another technique that will reduce acquisition time: Center the child menu, so that no item is more than total items/2 away from the mouse., as illustrated by Victor below:

Such a scheme, as Victor points out, doesn't work well with pull-down menus, unless the calling menu item is fairly far down the list. However, it is ideal for pop-up, contextual menus. Just ensure that the most important items are midway down the child menu, so they become the fastest to acquire. Question 9

The farther away the target is, the larger it must be to retain access speed. Not only did the industrial designers reduce the total size of the target, they reduced it in the very dimension that was most critical. Stupid, stupid, stupid. What they should have done was to curve the keyboard sharply upward toward the back end, so that merely lifting the finger a few degrees would access the numeric and function keys, aiding both precision and speed.

Question 10

What do the primary solutions to all these questions have in common?

You now know that it's Fitts' law. And you can use it in everyday design, whether you are building a new OS or laying out a new web page. When that default OK button, with only two characters, ends up really small, consider packing a few spaces in on either side to fill it out. If you have real control over your environment and are laying out a palette, make sure the user can access the tools by pinning against the screen edge. If you have menu bars at the top of the screen, use them! They are far more compact than a bunch of icons or buttons and, if you user-test, you will see they are faster. And if you work at Microsoft or Apple, consider listening to the people that have a clue when it comes to interaction design. They do exist. I've talked with them before. You might try talking with them, too.

I am indebted to Frank Ludolph and Craig Oshima for taking the test and finding a lot of additional correct answers, all of which I've attempted to include here.

If you would like to read more about Fitts' Law, I strongly recommend:

Walker, Neff and Smelcer, John (1990). "A Comparison of Selection Time from Walking and Bar Menus." Proceedings of CHI’90, Addison-Wesley, Reading, Mass., pp. 221-225.

As for how you did? If you can answer 10 out of 10 now, with understanding, and are prepared to apply the lessons learned, that's all that matters.

Links:

• Fitts's law